Le référentiel de mathématiques pour la physique - L0

Avant d'évaluer les compétences des étudiants ou de les accompagner dans leur remise à niveau, il est nécessaire de savoir ce dont on parle. Que faut-il savoir faire en maths pour les sciences pour réussir en physique en première année dans le supérieur?

Les tâches de mathématiques pour la physique

Nous sommes parti.e.s d'un découpage du savoir proche de celui fait en mathématiques dans le secondaire, mais nous nous sommes progressivement rendu compte que cela ne fonctionnait pas très bien. En effet, les tâches précises à réaliser en classe de physique-chimie et celles à réaliser en classe de mathématiques sont souvent un peu différentes. Les outils utilisés, et la manière de les utiliser diffèrent eux aussi un peu.

Partir des exercices de physique

Au début du travail de ce groupe, nous avons demandé à un enseignant de mathématiques de faire quelques exercices simples sur les logarithmes. L'objectif était de construire des exercices d'entraînement en contexte de mathématiques pour préparer nos étudiant.e.s aux exercices de physique. L'enseignant de mathématiques a alors rédigé un exercice typique de la classe de mathématique où l'on utilise les propriétés du logarithme pour travailler sur la décomposition en nombres premiers. Cet exercice a surpris les physicien.ne.s qui ne l'auraient jamais écrit "comme ça", avec le logarithme népérien. En classe de physique, lorsque l'on manipule des nombres avec les logarithmes, c'est que l'on s'intéresse à l'ordre de grandeur, c'est-à-dire à la puissance de 10 de ce nombre. En classe de physique, une simplification avec de vrais nombres, ce sera avec le logarithme décimal pour "attraper" la puissance de 10.

Nous avons donc repris le travail en partant de vrais exercices de physique ou de chimie, de lycée ou de première année d'université, dans lesquels nous avons isolé les tâches que nous considérerions être "des mathématiques". Nous avons aussi identifié les outils utilisés. Dans l'exemple présenté ci-dessous, les enseignant.e.s de physique considèrent que seule la ligne en dessous de "Descartes" correspond à une tâche de physique. Toutes les autres tâches à réaliser sont des tâches de "mathématiques pour la physique".

Référentiel des savoir-faire de m4s

Nous avons identifié dans un certain nombre d'exercices et d'annales d'examen les tâches de mathématiques pour la physique que les étudiant.e.s avaient à réaliser. En les comparant entre elles, et en cherchant à les catégoriser, nous avons constitué une douzaine de "types de tâche" que nous avons ensuite regroupé autour des 4 étapes de la modélisation (que l'on a appelées compétences).

Il faut bien garder en tête qu'il s'agit d'un référentiel pour l'entrée à l'université et que donc, au cours de leur scolarité, les étudiant.e.s devront savoir réaliser d'autres types de tâches. Pour chacun des types de tâche présentés dans le tableau ci-dessus, nous avons aussi identifié les outils et les techniques qu'un.e étudiant.e devait maîtriser pour réussir en physique dans le supérieur.

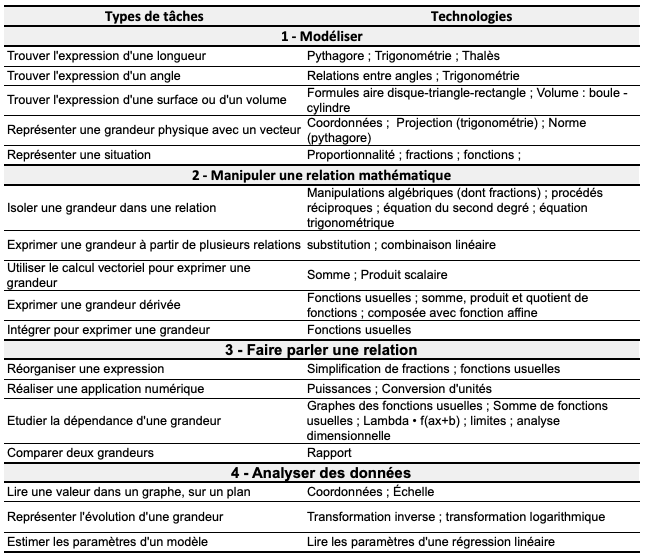
Référentiel des savoir-faire du projet M4S au 25/10/2020

Regard didactique : La différence entre les mathématiques et les mathématiques pour la physique

Les difficultés que nous avons rencontrées au début du projet pour s'accorder entre physicien.nes et mathématicien.ne.s nous rappellent à quel point le savoir est lié à la communauté dans lequel il vit. Un même objet de savoir (une loi, une formule, un concept) n'est pas utilisé exactement de la même manière, ni pour faire la même chose, dans une communauté ou dans une autre. La théorie anthropologique du didactique de Chevallard est une théorie qui permet de rendre compte de ces différences. Cette théorie permet par exemple de rendre compte des différences entre le savoir qui vit chez les mathématiciens et celui qui vit dans une classe de mathématiques de lycée. Il développe pour cela une analogie avec l'écologie en parlant d'écologie des savoirs. Nous retrouvons ces variations dans le savoir par rapport à la communauté qui l'utilise dans le savoir mathématique utilisé en classe de mathématique ou en classe de physique.

De nombreux travaux de didactique étudient ces différences. L'un des résultats marquant est que les physicien.ne.s manipulent des grandeurs quand les mathématicien.nes manipulent des fonctions. C'est ce qui permet en physique de garder la même lettre T lorsque l'on passe de \(T(x,y) \) à \(T(r,\theta)\) comme illustré dans l'exemple ci-dessous.

Notes et Références

• Pour plus d'informations sur les liens entre mathématiques et physique, vous pouvez consulter les articles du blog de Aude Caussarieu.