Datation de chondrites par la méthode dite "isochrone"
Par ftrouillet
—
Dernière modification
19/09/2017 09:50
On retrouve, dans les météorites de type chondrites, les éléments rubidium 87, strontium 87 et rubidium 86. Le rubidium 87 est radioactif 
-. Il se désintègre en strontium 87 qui est un isotope stable de l'élément strontium. La constante de désintégration radioactive
vaut 1,42.10-11 an-1. Nous allons déterminer l'âge de ces météorites en appliquant la méthode dite "isochrone".
Pour appliquer cette méthode, le système doit être resté clos depuis sa formation et il faut que la fermeture dure très peu de temps par rapport à l'âge à mesurer. De fait, il n'y a pas d'échange avec l'extérieur : la population de rubidium 87 diminue, la population de strontium 87 augmente et celle de strontium 86 reste constante.
Questions :
- Ecrire l'équation de désintégration radioactive du rubidium 87 et justifier l'emploi du rubidium 87 pour cette datation.
- Appliquer la loi de décroissance radioactive pour exprimer la relation entre la quantité initiale de rubidium 87 notée
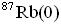et la quantité actuelle de rubidium 87 notée 
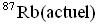en fonction de la constante de désintégration radioactive.
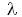- La quantité de strontium radiogénique
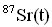produit par la désintégration radioactive correspond au nombre de désintégrations subies par le rubidium 87. En déduire la relation entre 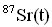, 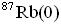et .
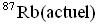- La quantité de strontium 87 présent actuellement dans une roche notée
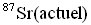est la somme du strontium 87 présent à l'origine 87Sr(0) et du strontium 87 radiogénique (produit par la désintégration radioactive). En déduire la relation entre 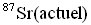, 87Sr(0) et .
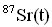- Montrer que l'on peut écrire :
- 87Sr(0) est inconnu. On résout ce problème en sachant que le rapport isotopique
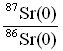est constant. Le strontium 86 est un isotope stable qui n'est ni radiogénique, ni radioactif : sa quantité est donc constante (elle n'a pas varié au cours du temps). Montrer alors que l'on peut établir l'expression :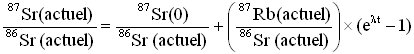 
- Les rapports de composition isotopiques d'une suite de 8 chondrites LL ont été obtenus directement à l'aide d'un spectrographe de masse. On obtient les valeurs suivantes. (D'après Minster et Allègre, 1981)
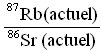 | 0,758 | 0,7255 | 1,52 | 1,49 | 1,555 | 1,685 | 0,1542 | 0,1533 |
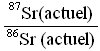 | 0,74864 | 0,7465 | 0,79891 | 0,79692 | 0,80152 | 0,80952 | 0,7091 | 0,70895 |
Ouvrir le tableur Open Office et créer une feuille de calcul comportant le tableau précédent.
- Insérer un diagramme X-Y (avec 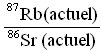en abscisse). Insérer la courbe de tendance (choisir régression linéaire). La courbe obtenue s'appelle une isochrone. Justifier ce nom.
- Déterminer l'ordonnée à l'origine et la pente de la droite obtenue (soit à l'aide d'une formule soit en affichant l'équation de la courbe de tendance).
- En déduire l'âge de ces météorites (c'est l'âge Rb-Sr du système solaire) et déterminer le rapport d'abondance isotopique
.
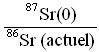