Variations du d18O des océans et variations du niveau marin

Mise à jour : 02/07/2002

Rédigé par J-M Greffion, Lycée A. Thierry, Blois 
et T.Lhuillier, Lycée Claude de France, Romorantin
Relu par : Gilles Delaygue, Université de Berne

Soit : 

V2 son nouveau volume

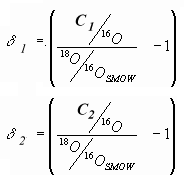
• C1 la concentration en ¹⁸O de l'océan
• V1 son volume initial
• Cg la concentration en ¹⁸O de la glace
• Vg le volume de glace fondu
• C2 sa concentration après fonte d'une certain volume de glace Vg

Exprimons la conservation de la quantité de ¹⁸O entre les deux états :

C2.V2 = C1.V1 + Cg.Vg  (1)

Supposons la variation de surface de l'océan comme négligeable (par rapport à S) à la suite de la fonte de Vg :

• Vg= S.Dh où Dh correspond à la variation du niveau de la mer. 
• V1= S.H où H correspond à la profondeur moyenne des océans. 
• V2 = S.(H +Dh)

(1) devient : C2.S(H +Dh)= C1.S.H + Cg.S.Dh
soit: 

C2.(H +Dh)= C1.H + Cg.Dh  (C2-C1).H = (Cg-C2).Dh   (2)

Exprimons maintenant les différences de concentrations en variations de d¹⁸O exprimé en pour mil.
 

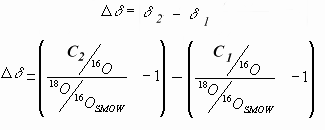Négligeons la variation de la quantité d'Oxygène 16 quand celle d'Oxygène 18 varie (ce qui est une très bonne approximation étant donné la masse globale du ¹⁶O). On obtient alors :

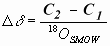
Or ¹⁸OSMOW = C1 (concentration en ¹⁸O dans l'océan actuel)

donc   C2 - C1 = C1.Dd    (3)

Remplaçons C2 - C1 par sa valeur dans l'équation (2). On obtient alors :

C1.Dd.H= (Cg - C2).Dh (4)

mais par ailleurs : d ¹⁸O_glace = (Cg/C1)- 1 (On considère là encore que ¹⁶O_glace = ¹⁶O_océan) 

D'où : Cg = (d¹⁸O_glace + 1) C1

En remplaçant Cg pas sa valeur dans (4), on obtient :

      C1.Dd.H= {[(d¹⁸O_glace + 1).C1]- C2}.Dh   C1.Dd.H = (d¹⁸O_glace.C1 + C1 - C2).Dh

Or C2- C1 = C1.Dd    (3)   et   C1-– C2 = - C1.Dd    (3)

L'équation devient alors: 

C1.Dd.H = (d¹⁸O_glace.C1- C1.Dd ).Dh

  C1.Dd.H = (d¹⁸O_glace- Dd).C1.Dh

Dd.H = (d¹⁸O_glace- Dd).Dh

Finalement  :                Dh = H . Dd / (d¹⁸O_glace - Dd)

Par soucis de simplification des calculs, on peut négliger Dd au dénominateur et la formule devient: 

Dh = H . Dd / d¹⁸O_glace

Dans le cas d'une analyse du d¹⁸O des carbonates des foraminifères benthiques, la variation de celui-ci est égale à la variation du d¹⁸O des océans. (voir la signification du d¹⁸O). 
Pour une variation du d¹⁸O de -1 pour mille (correspondant à une fonte de glaces), en supposant que les calottes ont une composition isotopique moyenne d¹⁸O = -40 pour mille, et l'océan global une profondeur moyenne de 4000 m, cette variation du d¹⁸O correspond à une variation du niveau marin de :

Dh = 4000 x (-–1) / - 40 = + 100 m

Une variation du d¹⁸O de l'eau des océans (du d¹⁸O des carbonates des foraminifères benthiques) de 1 pour mille correspond à une variation du niveau marin de 100 m environ.
 

Version simplifié du calcul.

La fonte de glaces très pauvres en ¹⁸O aux pôles a pour conséquence une élévation du niveau marin, un appauvrissement corrélatif de l'eau de mer en H₂¹⁸O et donc une baisse du d¹⁸O des océans.
Cherchons à établir la relation entre la variation Dh du niveau de la mer et la variation Dd du d¹⁸O des océans.

Soit : 

• C1 la concentration en ¹⁸O de l'océan


• V1 son volume initial
• Cg la concentration en ¹⁸O de la glace


• Vg le volume de glace fondu
• C2 sa concentration après fonte d'une certain volume de glace Vg


• V2 son nouveau volume

Exprimons la conservation de la quantité de ¹⁸O entre les deux états :

C2.V2 = C1.V1 + Cg.Vg (1)

La relation entre les d¹⁸O et les concentrations étant linéaire, on peut remplacer les concentrations par les deltas. 

d2 . V2 = d1 . V1 + dg . Vg  (2)

Supposons la variation de surface de l'océan comme négligeable (par rapport à S) à la suite de la fonte de Vg :

• Vg= S.Dh où Dh correspond à la variation du niveau de la mer. 
• V1= S.H où H correspond à la profondeur moyenne des océans. 
• V2 = S.(H +Dh)

(2) devient :

d2 . (H +Dh) = d1 . H + dg . D h  (3) 

  (d2 - d1). H = (dg - d2) .Dh   (4) 

Comme ¦dg¦ >>>> ¦d2¦

(4)  Dd . H = dg .Dh   (5) 

Soit : 

Dh = H . Dd / dg

Dans le cas d'une analyse du d¹⁸O des carbonates des foraminifères benthiques, la variation de celui-ci est égale à la variation du d¹⁸O des océans. (voir la signification du d¹⁸O). 
Pour une variation du d¹⁸O de -1 pour mille (correspondant à une fonte de glaces), en supposant que les calottes ont une composition isotopique moyenne d¹⁸O = -40 pour mille, et l'océan global une profondeur moyenne de 4000m, cette variation du d¹⁸O correspond à une variation du niveau marin de :

Dh = 4000 x (-1) / - 40 = + 100 m

Une variation du d¹⁸O de l'eau des océans (du d¹⁸O des carbonates des foraminifères benthiques) de 1 pour mille correspond à une variation du niveau marin de 100m environ.