Atmosphère, atmosphère !
L'atmosphère d'une planète est constituée d'un mélange de gaz caractérisé par sa composition chimique, sa température et sa pression. Pour répondre à la question posée, il faut connaître d'abord la température ce qui permet de définir la vitesse quadratique moyenne des molécules qui constituent l'atmosphère. Ensuite il faut comparer ces vitesses avec la vitesse de libération de la planète considérée.
- Témpérature d'un gaz parfait :
Un gaz parfait est un gaz à basse pression dont les constituants sont suffisamment éloignés les uns des autres pour pouvoir négliger les interactions d'ordre électrostatique entre eux. La température du gaz est la perception macroscopique de l'agitation incessante des particules le constituant. La théorie cinétique des gaz parfaits indique que la vitesse quadratique moyenne v* d'un gaz (v*² est égal à la moyenne des carrés des vitesses) est liée à la température absolue (en Kelvin) de ce gaz :
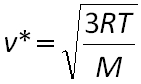 avec R : constante des gaz parfaits (R = 8,314 J.K-1.mol-1); M : masse molaire de la molécule en kg/mol et v* en m/s.
avec R : constante des gaz parfaits (R = 8,314 J.K-1.mol-1); M : masse molaire de la molécule en kg/mol et v* en m/s.
On peut ainsi calculer les vitesses quadratiques moyennes de quelques gaz parfaits en fonction de la température :
| Molécules | He | H2 | O2 | N2 |
| M (en kg/mol-1) | 4.10-3 | 2.10-3 | 32.10-3 | 28.10-3 |
| v* (en m.s-1) à T = 100 K (soit à -173,15 °C) | 789,6 | 1116,7 | 279,2 | 298,5 |
| v* (en m.s-1) à T = 200 K (soit à -73,15 °C) | 1116.7 | 1579,3 | 394,8 | 422,1 |
| v* (en m.s-1) à T = 250 K (soit à -23,15 °C) | 1248,5 | 1765,7 | 441,4 | 471,9 |
| v* (en m.s-1) à T = 300 k (soit à 26,85 °C) | 1367,7 | 1934,2 | 483,6 | 516,9 |
| v* (en m.s-1) à T = 350 k (soit à 76,85 °C) | 1477,3 | 2089,2 | 522,3 | 558,4 |
| v* (en m.s-1) à T = 400 k (soit à 126,85 °C) | 1579,3 | 2233,5 | 558,4 | 596,9 |
Pour obtenir une feuille de calcul au format open office pour calculer les vitesses quadratiques moyennes, cliquer ici.
La probabilité qu’une molécule ait une vitesse supérieure à la vitesse de libération est d’autant plus grande que sa vitesse quadratique est proche de la vitesse de libération de l'astre considéré.
- Vitesse de libération d'un astre :
La vitesse de libération d'un astre (escape velocity en anglais) est la vitesse minimale qu'il faut communiquer à un corps, quelle que soit sa masse, pour qu'il échappe définitivement à l'attraction gravitationnelle de cet astre (ceci en supposant négligeable la résistance de l'atmosphère).
L'énergie mécanique du corps est la somme de son énergie cinétique et de son énergie potentielle de pesanteur :
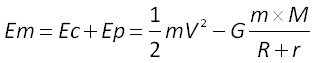
avec G : constante de gravitation ; m : masse du corps ; M : masse de l'astre ; R : rayon de l'astre et r : distance à la surface de l'astre.
L'énergie mécanique est conservée au cours du temps car la seule force qui s'exerce ici est la force gravitationnelle qui est conservative. On peut donc écrire :
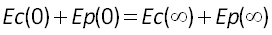
À une distance infinie, la vitesse du corps est nulle (car on cherche la vitesse minimale pour échapper au champ gravitationnel). de plus son énergie potentielle de pesanteur est nulle car r tend vers l'infini. Son énergie mécanique est donc nulle. On a donc Em = 0.
La vitesse de libération (en m.s-1) à partir du sol est la vitesse pour r = 0 (surface de l'astre). On a donc :
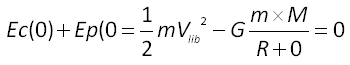
Ce qui donne :
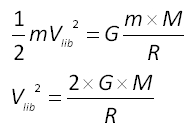
Soit : 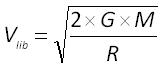 avec G : constante de gravitation (G = 6,67.10-11 N.m2kg-2) : M : masse de l'astre en kg et R : rayon de l'astre en m.
avec G : constante de gravitation (G = 6,67.10-11 N.m2kg-2) : M : masse de l'astre en kg et R : rayon de l'astre en m.
On peut remarquer que cette vitesse ne dépend pas de la masse du corps et que plus l'astre est petit et massif, plus cette vitesse est grande.
Calculons les vitesses de libération pour quelques corps :
| Astre | Masse (en kg) | Rayon (en km) | Vitesse de libération (en km.s-1) |
| Mercure | 3,27.1023 | 2 439 | 4,23 |
| Venus | 4,85.1024 | 6 052 | 10,33 |
| Terre | 5,97.1024 | 6 378 | 11,18 |
| Lune | 7,34.1022 | 1 740 | 2,37 |
| Mars | 6,37.1023 | 3 397 | 5,00 |
| Phobos | 1,07.1016 | environ 25 | 7,55.10-3 |
| Jupiter | 1,90.1027 | 71 492 | 60,62 |
| Europe | 4,8.1022 | 1 561 | 2,02 |
| Saturne | 5,68.1026 | 60 268 | 35,45 |
| Titan | 1,34.1023 | 2 570 | 2,64 |
| Uranus | 8,68.1025 | 25 560 | 21,28 |
| Neptune | 1,02.1026 | 24 800 | 23,42 |
| Pluton | 1,31.1022 | 1 150 | 1,23 |
| Soleil | 1,99.1030 | 696 000 | 617,6 |
- Atmosphère ou pas ?
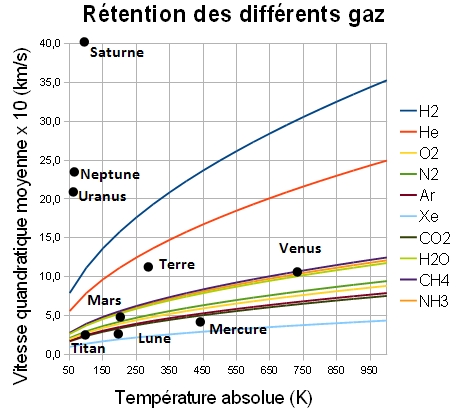
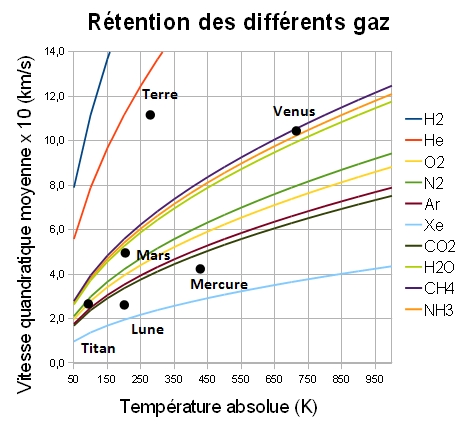
Si la vitesse quadratique moyenne d'un constituant de l'atmosphère d'un astre de température moyenne T est au minimum 10 fois supérieure à sa vitesse de libération alors ce gaz peut s'échapper. Dans les diagrammes suivants (le 2ème diagramme est un « zoom » du 1er), on a représenté l'évolution des vitesses moyennes de différents gaz (x 10) en fonction de leur température. On y a placé quelques planètes et satellites connaissant leur température moyenne et leur vitesse de libération.
Un astre ne pourra retenir un gaz que si le point qui le représente est situé au-dessus ou au voisinage de la courbe correspondant à ce gaz. Si on considère un astre particulier, on peut donc en déduire que les gaz situés au-dessus du point qui le représente dans le diagramme ont progressivement échappé à son attraction gravitationnelle.