Le corps noir

• Quelle que soit sa température, un corps émet de la lumière (sauf s'il est à 0°K). Plus il est chauffé et plus il émet de lumière.

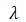Considérons par exemple, un morceau de fer. Lorsqu'il est froid, le fer n'émet pas de lumière visible ; il s'agit d'un rayonnement infrarouge invible à l'oeil nu (longueur d'onde>700 nm). Si on le chauffe, il devient rouge et on commence à apercevoir une émission de lumière dans la partie rouge du spectre visible (400 nm <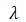< 700 nm). Si on augmente encore la température, il devient jaune, puis blanc et enfin bleu. Ce comportement est universel et ne dépend pas de la nature de la matière utilisée pour faire l'expérience.

• Par conséquent, lorsqu'un corps est en équilibre thermique, les propriétés de son rayonnement sont parfaitement déterminées par la seule donnée de la température. Il existe donc une relation entre la longueur d'onde du rayonnement émis et la température.

• Pour décrire les caractéristiques du rayonnement émis par un objet à une température T, il faut s'assurer que l'énergie incidente (provenant de la lumière ambiante) réfléchie par l'objet ne vienne pas s'ajouter à l'énergie rayonnée émise par l'objet en raison de sa température. Pour cela, on considère un objet qui absorberait toute l'énergie électromagnétique qu'il recevrait, sans en réfléchir ni en transmettre. Cet objet est appelé corps noir. C'est un objet idéal qui absorberait toutes les longueurs d'onde et qui émettrait un rayonnement électromagnétique qui ne dépend que de sa température. La lumière (onde électromagnétique) serait absorbée totalement par cet objet qui devrait donc apparaître noir (d'où son nom). On peut considérer un corps noir comme un objet recouvert d'une épaisse couche de noir de fumée. L'énergie apportée par la lumière incidente va contribuer à amener le corps noir à la température T et étant intégralement absorbée, cette énergie incidente ne se mélange pas avec l'énergie rayonnée.

La loi empirique de Stefan-Boltzmann (1879) permet d'exprimer la puissance rayonnée P_r (c'est-à dire la quantité d'énergie rayonnée émise chaque seconde) par unité de surface du corps noir. P_r s'exprime en W.m^-2.

Cette loi énonce que P_r augmente proportionnellement à la puissance quatre de la température absolue du corps.

P_r = ×T⁴  (avec T : température absolue en K)

Wilhlem Wien réalisa une série d'expérience sur le rayonnement du corps noir. Il utilisa un four hermétiquement fermé et isolé qu'il perça d'un minuscule trou pour en étudier le rayonnement électromagnétique qui s'échappait. Il put ainsi connaître la température à l'intérieur du four et établir une loi empirique (1896) qui relie le spectre d'émission d'un corps noir et sa température. Ce spectre d'émission est en forme de cloche. La loi de Wien permet de déterminer la longueur d'onde (en m) pour laquelle le rayonnement du corps noir est le plus intense.

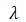= 2,898 x 10^-3 / T

 

Quelques applications de la loi de Wien

Considérons que le Soleil est un corps noir. Son pic d'émissivité se situe à 500 nm. En appliquant la loi de Wien, on en déduit une température de surface de 5800 K.

La température de surface de la Terre étant de 288 K, on en déduit que l'essentiel du rayonnement se fait dans l'infrarouge.

Retour