3compart_600Ma
Construction d'un modèle complexe dérivé de GEOCARB II
Modèle de Berner
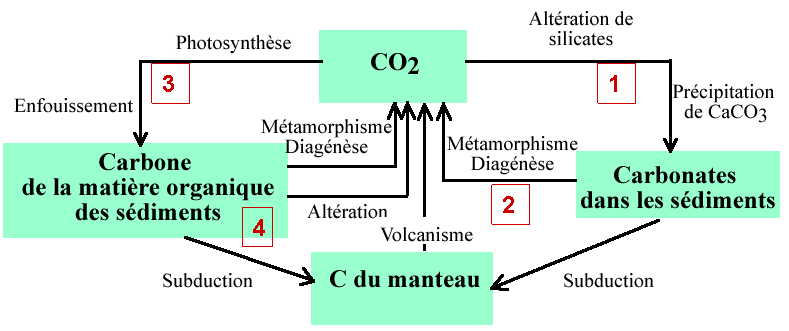
Modèle du cycle du carbone à long terme de Berner (Nature 426, 323-326, 2003)
Ce modèle prend en compte :
- l'altération des silicates, des carbonates et de la matière organique
- le dégazage thermique du CO2 par le volcanisme, le métamorphisme et la diagenèse
- le piègeage de la matière organique et des carbonates dans les sédiments
mais il ne prend pas en compte l'altération et la précipitation des carbonates car sur le long terme ces deux processus se compensent
La flèche 1 correspond au piégeage du dioxyde de carbone lors de l'altération des silicates, puis à la précipitation sous forme de carbonates dans les océans. .L'équation simplifiée peut s'écrire :
CO2 + CaSiO3 <=> CaCO3 + SiO2
La flèche 3 correspond à la photosynthèse nette(photosynthèse moins respiration)
elle équivaut à enfouissement de la matière organique (CH2O) dans les sédiments. Cette matière organique est éventuellement transformée en kérogène, huiles, gaz, charbon. L'altération de cette matière organique lorsqu'elle est exposée à l'érosion sur les continent ou lorsqu'elle est entraînée dans des zones de subduction libère du dioxyde de carbone (flèche 4)
Présentation du modèle dérivé de GEOCARB II
Le modèle a été proposé sous le logiciel Stella par le doyen John T Snow à l'université d' Oklahoma, , il est basé sur les séries GEOCARB publiées par Berner (Université de Yale) en 1991 et 1994. Il s'agit d'une modélisation du cycle du carbone à long terme (centaines de milliers à centaines de millions d'années, petits flux et gros réservoirs) par opposition au cycle à court terme (années à milliers d'années, gros flux et faibles temps de séjour).
Le modèle appartient tout comme les autres modèles du cycle à long terme sur lesquels nous avons travaillé au groupe des modèles qui ne permettent pas d'étudier des évènements dans lesquels un déséquilibre temporaire océan atmosphère jouerait un rôle (trapps du Dekkan par exemple). Les valeurs initiales correspondent aux valeurs actuelles, ce qui n'est pas rigoureusement correct mais n'influence pas beaucoup les simulations puisqu'un équilibre s'établit après quelques millions d'années.
En raison des échelles de temps très longues, les échanges de carbone entre "l'océan superficiel, l'océan profond, l'atmosphère, et la biosphère" peuvent être considéré à l'équilibre. L'ensemble "hydrosphère, biosphère, atmosphère" est rassemblé dans un unique réservoir que l'on nomme "carbone océans/atmosphère/biosphère"
Le modèle est conçu pour simuler les temps depuis 0 (juste avant le début du Cambrien) jusqu'à 600 Millions d'années (présent).
Structure du modèle
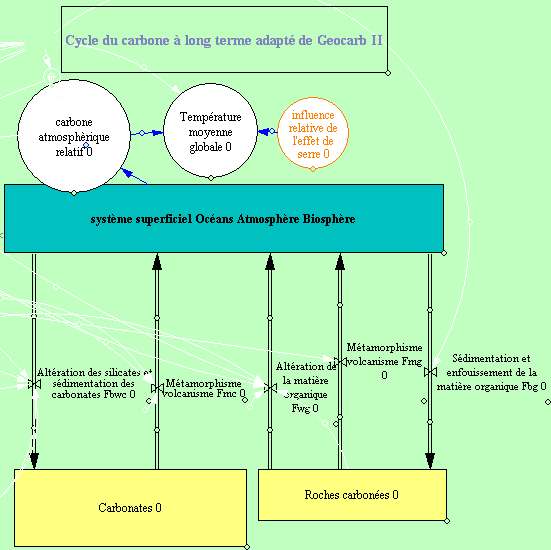
Informations techniques pour la construction du modèle
- Construire le modèle numérique en utilisant le logiciel Vensim (voir la prise en main de ce logiciel) :
- Lancer l'application Vensim
- Créer un nouveau modèle : choisir la période de 0 à 600 millions d'années et le pas 0.125
- Construire les compartiments "Système superficiel", "Carbonates", roches carbonées"
- Construire les 6 flux
- Mettre en place les "convertisseurs".
- Voir ci-dessous les données numériques ayant servi à la construction du modèle.
- Enregistrer le modèle et tester le.
Tester le modèle 3comp_600Ma.vmf contenu dans l'archive 3comp_600Ma.zip avec Vensim Model Reader . Dans cette archive, vous avez également le modèle enregistré au format mdl qui s'ouvre avec Vensim PLE (mais qui ne fonctionne pas). Cela permet d'analyser les équations
Equations du modèle 3comp_600Ma.mdl
1- Durée de validation du modèle
- Début du modèle INITIAL TIME = 0 Million d'années
- Fin du modèle FINAL TIME = 600 Millions d'années
- Pas de la simulation TIME STEP = 0.125
2- Trois réservoirs
- INIT carbone océans/atmosphère/biosphère = 2.8e18 moles
- INIT carbone dans les roches carbonées = 1250e18 moles
- INIT carbone dans les carbonates = 5000e18 moles
3- Flux modélisés :
-
Fmc = Dégazage accompagnant le métamorphisme et/ou l'altération volcanique des carbonates
Fmc = fg*fc*kmc*5000e18
-
Fbc = Sédimentation, enfouissement des carbonates
Fbc = Fwc+fa*fb*fe*fr*(fd^0.65)*6.7e18
-
Fwc = Altération des carbonates
Fwc = fb*fa*fd*fe*kwc*Carbonates
Afin de se rapprocher du modèle de Berner Géocarb III, Fbc et Fwc seront regroupées en un seul flux Fbwc.
-
Fbwc = Altération des silicates et précipitation des carbonates
Fbwc = fb*fa*fd*fe*fr*(fd^0.65)*6.7e18
-
Fmg = Dégazage accompagnant le métamorphisme et/ou l'altération volcanique de la matière organique
Fmg = fg*kmg*1250e18
-
Fbg = Sédimentation enfouissement de la matière organique. Fbg est fixe, sur la base des données de Berner et Canfield (1991).
Fbg =1e+018*(4.37+6.15*EXP(-((Time-300)^2)/1573)+2.61*EXP(-((Time-500)^2)/9852.5))
-
Fwg = Altération de la matière organique
Fwg = kwg*fr*fd*carbone organique
4- Facteurs influençant les flux
-
fb est une "fonction feedback" qui traduit l'influence des taux d'altération sur CO2,
fb = w^0.65*EXP(-0.09*12.9*(1-Time/600))*((c relatif^(0.09*6))*SQRT(c relatif)*switch2+switch1*(c relatif^0.54)*(2*c relatif/(1+c relatif))^0.4)
-
fd sur le site de l'Oklahoma est annoncé comme étant le rapport des carbonates exposés au-dessus du niveau de la mer par rapport au présent x le rapport du flux des rivières vers les océans (runoff continental) par rapport au présent ce qui ne correspond pas à l'équation entrée dans le modèle, puisque la valeur actuelle est à 0.15 au lieu de 1, il serait prudent de ne pas jouer avec ce paramètre
fd = graph(time)
([(0,0)-(600,10)],(0,1),(60,1),(120,1),(180,1),(240,1),(300,1),(360,1),(420,1),(480,0.15),(540,0.15),(600,0.15) )
-
fa est le rapport des carbonates exposés au-dessus du niveau de la mer par rapport au présent
fa = graph(time)
fa = (-0.776683 + 0.0973342*Time - 0.00244251*Time^2 + 2.96725e-005*Time^3 - 1.97654e-007*Time^4 + 7.75275e-010*Time^5 - 1.83486e-012*Time^6 + 2.57012e-015*Time^7 - 1.95746e-018*Time^8 + 6.23356e-022*Time^9)
-
fr sur le site de l'Oklahoma est annoncé comme étant le rapport du relief topographique continental moyen par rapport au présent, ce qui ne correspond pas à l'équation entrée dans le modèle, puisque la valeur actuelle est à 3.5 au lieu de 1, il serait prudent de ne pas jouer avec ce paramètre
fr = graph(time)
fr = ([(0,0)-(600,10)],(0,1),(400,1),(600,3.5) )
-
fe exprime l'influence de l'activité biologique des sols due aux plantes terrestres sur le taux d'altération
fe = graph(time)
([(0,0)-(600,2)],(0,0.163),(31.6,0.175),(158,0.175),(189,0.188),(221,0.306),(253,0.469),
(284,0.594),(316,0.756),(347,0.756),(366.972,0.756),(379,0.756),(411,0.756),(442,0.756),
(474,0.756),(505,0.956),(537,1.07),(568,1.08),(600,1.08) )
-
fg est le rapport du taux de dégazage dans le passé par rapport au présent (en grande partie une fonction du mouvement tectonique des plaques c'est à dire du taux d'expansion des océans)
fg = graph(time)
([(1,0.8)-(600,2)],(0,1),(50,1),(100,1.7),(120,1.5),(181.651,1.51579),(216.514,1.48421),(249.541,1.48421),
(256.881,1.19474),(275.229,1.18421),(290.425,1.23684),(301.416,1.23684),(321.101,1.16842),(377.982,1.15789),
(420.483,1.16842),(468.11,1.17368),(475.437,1.49474),(502.914,1.45263),(523.064,1.45263),(541.382,1.41579),
(579.85,1.12632),(600,1) )
-
fc exprime l'influence de la profondeur des carbonates sur le taux de dégazage (effet du plancton).
fc = graph(time)
([(0,0)-(600,2)],(0,0.76),(360,0.76),(420,0.78),(480,0.85),(540,0.92),(600,1) )
5 - Convertisseurs :
kmc = 0.00133
kwc = 0.00267
kmg = 0.001
kwg = 0.00030
Contacter l'auteur :
