La décroissance radioactive
Par ftrouillet
—
Dernière modification
19/09/2017 09:50
Désintégration du noyau radioactif
- Un noyau radioactif est un noyau instable subissant spontanément une transformation appelée désintégration permettant un retour à la stabilité. Il ne "vieillit" donc pas puisqu'il se transforme sans subir de modifications progressives. Cela signifie qu'un noyau radioactif créé il y a 10 ans a autant de chance de se désintégrer à cet instant qu'un noyau identique venant d'être créé.
- Pour un noyau donné, le phénomène de désintégration est donc aléatoire et imprévisible. Par contre, l'évolution statistique d'une population de noyaux répond à une loi de probabilité bien déterminée.
Loi de décroissance radioactive d'une population
- Soit N0, le nombre de noyaux radioactifs tous identiques initialement présent dans l'échantillon.
- Au bout d'un temps t, la population de noyaux a diminué. Soit N(t), le nombre de noyaux radioactifs tous identiques présent dans l'échantillon à la date t.
- Le nombre moyen de désintégration (variation de population
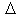N) est proportionnel à la population existante N(t) et à la durée de mesure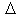t. On a donc :
N = -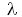 
x N(t) xt (avec coefficient de proportionnalité appelé constante radioactive)
- Si la durée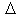t tend vers 0, on obtient l'équation différentielle suivante :
avec 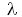en s-1
La solution de cette équation différentielle donne la loi de décroissance radioactive :
Constante de temps
- La constante de temps (en s) est définie par :
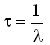. C'est la durée de vie moyenne d'un noyau. (On parle de "moyenne" car certains noyaux se désintègrent plus rapidement que d'autres.)
- La loi de décroissance radioactive est donc :
Demi-vie d'un élément radioactif
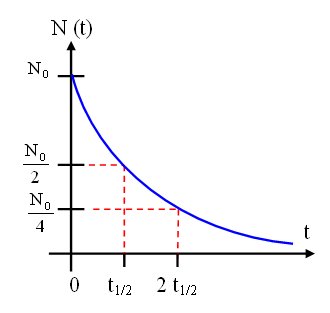
Un noyau radioactif est plus souvent caractérisé par sa demi-vie notée t1/2 que par la durée
. La demi-vie est la durée au bout de laquelle la population initiale N0 est divisée par deux.
On a N (t1/2) = N0/2 donc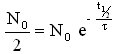 
D'où : t1/2 = ln2
ex : t1/2 (thorium 230) = 7,5.104 ans ; t1/2 (carbone14) = 5 730 ans
t1/2 (iridium 194) = 19 heures ; t1/2 (iode 131) = 8,1 jours
