Datation au carbone 14 - FICHE ELEVE
Par ftrouillet
—
Dernière modification
19/09/2017 09:50
On retrouve dans une grotte ornée, des restes de foyer contenant des morceaux de charbon de bois. On mesure l'activité de 40 g de charbon : on trouve une activité A de 1 Bq.
Nous allons tenter de dater cet échantillon par la méthode au carbone 14.
Questions :
- Pourquoi la méthode au carbone 14 peut-elle être utilisée ici ?
- Calculer la population de
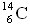dans l'échantillon de charbon. On notera N14 cette population. - Déterminer la population de
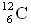dans l'échantillon. On supposera qu'elle est égale au nombre d'atomes de carbone N (tous isotopes confondus) contenus dans l'échantillon car N14 est négligeable devant N. On notera N12 cette population. - Calculer le rapport r =
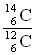de populations. On rappelle que le rapport intial est r0 = 
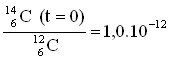. Calculer la valeur de r/r0 pour cet échantillon. - La demi-vie t1/2 de l'isotope 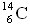est en théorie de 5730 ans
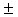40 ans. Exprimer la relation entre r, r0 et la période de demi-vie t1/2 en appliquant la loi de décroissance radioactive. - Tracer la courbe représentant les variations de r/r0 en fonction du temps.
- En utilsant le rapport r/r0 calculé question 4, déterminer graphiquement l'âge de l'échantillon.
- Retrouver ce résultat par le calcul.
- Il existe une incertitude de 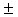40 ans sur la période radioactive du 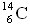. Quelle variation sur l'âge de l'échantillon cette incertitude induit-elle ? Donner un encadrement de l'âge de l'échantillon.
