Les fractions
[En cours de rédaction]
Manipuler des fractions

Au départ les fractions sont associées au partage d'un gâteau. Les fractions permettent en fait de construire de nouveaux concepts en mathématiques (proportionnalité et pente d'une droite, exposants négatifs) et en sciences (vitesse en physique, masse volumique, nombre de moles, ...). La plupart des applications numériques demandent aux étudiants de simplifier des fractions en utilisant aussi les puissances de 10.
Plusieurs savoir-faire du référentiel maths4sciences L0 sont associés à la manipulation des fractions :
- Simplifier une fraction (calcul littéral ou numérique)
- Isoler une grandeur dans une équation (calcul littéral)
- Calculer une application numérique
Maths versus sciences
Des chiffres ou des lettres?
En mathématiques au collège les élèves manipulent beaucoup les fractions avec des nombres. Ils réalisent des opérations élémentaires (+, -, x, ÷) sur les fractions. Les fractions vont être utilisées ensuite dans des situations de proportionnalité comme les pourcentages ou le théorème de Thalès.
Les élèves vont aussi avoir à simplifier des fractions avec des nombres. Vrai?
En physique un très grand nombre de lois et de formules font intervenir des fractions : optique géométrique (grandissement, relations de conjugaison), électricité (loi d'Ohm pour des résistances en parallèle). L'objectif des calculs est alors de simplifier l'écriture ou bien d'isoler une grandeur pour l'exprimer en fonction des autres grandeurs du problème.
Les calculs sont le plus souvent menés en littéral jusqu'à l'application numérique. À ce moment là les élèves doivent faire un groupe avec tous les nombres et un autre avec toutes les puissances de 10, puis calculer la valeur de ces deux groupes, et enfin donner le résultat, avec la bonne unité!
Les unités
En mathématiques les fractions n'ont pas d'unité!
En physique et en chimie, des fractions sont utilisées pour construire des concepts relationnels comme la vitesse, la masse volumique, la densité, ... Ces grandeurs ont souvent une unité.
Simplifier une fraction
En mathématiques, simplifier une fraction c'est "enlever les produits par 1".
Les étudiants ont peu d'entraînement au calcul littéral avec des fractions en cours de mathématiques.
Les erreurs fréquentes des étudiants

→ Et les moyens de les aider!
- Non respect des priorités opératoires entre puissances et parenthèses : (ab)^2=ab^2
- → Faire retravailler les puissances et la distributivité
- La fraction de fraction n'est pas comprise
-
→ Faire réécrire en transformant la barre de fraction au niveau du signe = par un symbole de division :
(a/b)/c = a/b ÷ c
a/(b/c) = a ÷ b/c
-
- Les symboles utilisés ne sont pas compris comme dx/dt = x/t ou bien sin a / sin b = a/b.
- → Garder les parenthèses dans les fonctions et le signe ×
- → Attirer l'attention des étudiants sur les implicites : parenthèses sous entendues, signe × sous entendu
- La simplification des fractions n'est pas spontanée chez les étudiants qui gardent parfois des fractions compliquées sur plusieurs lignes de calcul
- → Simplifier c'est trouver une écriture facile à comprendre et à manipuler dans un calcul
- Quand "simplifier" et jusque où? : n/1 ou n^2/n en dernière ligne du calcul
- → On simplifie car multiplier par a/a, c’est multiplier par 1 donc, on peut supprimer de l’écriture a/a
- → Repérer les facteurs communs pour factoriser le numérateur et le dénominateur.
- Changement de registre : "prendre une fraction d'un nombre c'est multiplier ce nombre par la fraction" : non acquis
- → Expliquer que dans une phrase “de” signifie souvent “multiplier” et “par” signifie souvent “diviser”
Exemple : prendre les ¾ de 20 kg donnera le calcul suivant : ¾ × 20
- → Expliquer que dans une phrase “de” signifie souvent “multiplier” et “par” signifie souvent “diviser”
DES Quiz en contexte de maths

Niveau 1 - se souvenir
Niveau 2 - Comprendre
Ecrire mathématiquement une fraction

Repérer les écritures équivalentes d'une fraction

Variables didactiques : lettres utilisées, fraction de fraction, utilisation (ou pas) du signe multiplié entre les lettres, valeurs numériques, signe moins (en haut, en bas, devant)
Reconnaître une fraction simplifiée
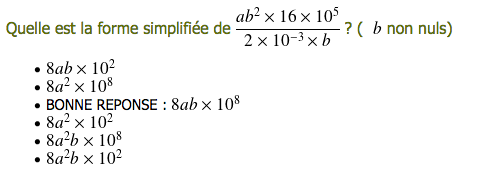
Variables didactiques : fractions de nombres et/ou lettres et/ou fonctions
Niveau 3 - appliquer
Simplifier une fraction
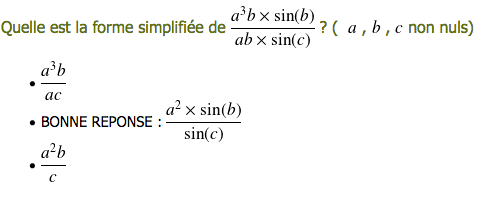
Variables didactiques : nombres, lettres, fonctions ; écriture (ou pas) du signe multiplier
Isoler une variable

Variables didactiques : x est déjà seul, ou pas. Ce n'est pas x qu'il faut isoler.
Niveau 4 - Analyser
Que se passe-t-il si?
Des Quiz en contexte de physique
Niveau 2 - comprendre
Traduire un texte en une expression mathématique

Niveau 3 - Appliquer
Trouver une valeur en utilisant une relation de proportionnalité

