Comment calculer l'âge grâce au carbone 14 ?
Rédigé par Thierry Lhuillier, Lycée Claude de France, Romorantin
 |
A partir d'un exercice de Gilles Delaygue Laboratoire de Physique du Climat et de l'Environnement, Université de Berne |
Principe de la datation
 Université d'Oxford, Unité de mesure radiocarbone, avec la permission de l'auteur. |
La matière organique est formée notamment de carbone, incorporé directement (organismes autotrophes) ou indirectement (organismes hétérotrophes) à partir du CO2 atmosphérique (dans les océans, les carbonates dissous proviennent de l'atmosphère). Le CO2 atmosphérique contient principalement l'isotope stable 12C, mais également les isotopes 13C (stable) et 14C (instable) en très petites quantités : 1 atome 13C pour 100 atomes de 12C et 1 atome 14C pour 1012 atomes de 12C environ. Le carbone 14 décroît par radioactivité, avec une 'demi-vie' d'environ 6000 ans. Il est produit dans la haute atmosphère par bombardement cosmique sur l'azote N2. Dans l'atmosphère, la décroissance du 14CO2 équilibre cette production, et le rapport 14C/12C du CO2 est constant. Tant qu'un organisme est vivant, il échange du carbone avec l'atmosphère et le rapport 14C/12C de sa matière organique est constant. Dès que cet organisme meurt, il n'échange plus avec l'atmosphère et ce rapport 14C/12C commence à décroître. |
La décroissance du 14C suit une loi cinétique du premier ordre. Pour un nombre N d'atomes 14C, le taux de décroissance dN/dt est proportionnel à N :
dN/dt = -lambda * N
où lambda est une constante physique de décroissance radioactive.
L'intégration temporelle de cette loi conduit à une forme exponentielle :
N = N0 . exp(-lambda*t) (1)
où N0 est le nombre initial d'atomes 14C et N le nombre au temps t (âge).
Lorsque les mesures sont faites par spectrométrie (voir ci-dessous), elles fournissent le rapport 14C/12C d'un échantillon. Comme le nombre d'atomes 12C est resté constant pour un échantillon donné, on peut diviser N par le nombre d'atomes de 12C dans l'équation (1) qui devient :
R = R0 . exp(-lambda*t) (2)
où R0 est le rapport initial (équilibre avec l'atmosphère) et R le rapport au temps t.
Cette loi exponentielle est caractérisée par un temps de 'demi-vie' appelé période T, au bout duquel la moitié de la quantité initiale de 14C a disparu. Au temps T, on a donc :
R = R0/2 = R0 . exp(-lambda*T)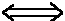
1/2 = exp(-lambda*T)
en prenant le logarithme :
ln(1/2) = - ln(2) = - lambda*T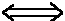T = ln(2) / lambda
Pour le 14C, la période T toujours utilisée est égale à 5568 ans. 1/lambda correspond alors à 8033 ans. Cette valeur de la période correspond à celle proposée par l'inventeur de la méthode carbone 14 (W.F.Libby). Depuis, cette période a été corrigée à 5730 ans (1/lambda = 8267 ans).
Pour calculer l'âge, on utilise alors cette constante et l'équation (2) devient :
R / R0= exp(-lambda*t)
En prenant le logarithme,
ln(R / R0) = -lambda*t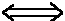 ln(R0/R) = lambda*t
donc l'âge :
t = ln(R0/R) . 1 / lambda = 8033 . ln(R0/R)
Principe de mesure
Le rapport isotopique R = 14C/12C peut être mesuré de deux façons différentes.
Par comptage des particules 'Bêta' issues de la désintégration du 14C
On mesure le rayonnement Bêta issu d'un échantillon de masse connue (nombre d'atomes 12C connu) pendant une longue période (plusieurs mois). Cette 'radioactivité' est proportionnelle au nombre d'atomes de 14C, que l'on peut ainsi déterminer.
Par mesure du rapport isotopique par spectrométrie de masse
L'échantillon est réduit en graphite ou en CO2 gazeux, analysé dans un spectromètre de masse. Cette technique permet la mesure d'un très petit nombre d'atomes de carbone. Elle présente donc un avantage sur le comptage Bêta lorsqu'on ne dispose que de très faibles quantités d'échantillon, ou que l'échantillon est vieux et contient peu de 14C.
La limite de détection des spectromètres fixe ainsi la limite de la technique 14C aux derniers 40 000 ans environ.