LES LOIS DE KEPLER
|
Johannes Képler (1571 - 1630) fut l'assistant de l'astronome danois Tycho Brahé. En 1600, à Prague, Brahé lui demanda de calculer l'orbite précise de Mars. En effet, il avait remarqué une excentricité de sa trajectoire, ce qui était considéré comme une anomalie à une époque où l'on pensait que les orbites des planètes étaient parfaitement circulaires. Il fallut six ans à Képler pour achever son travail. A partir d' observations très précises, il établit de façon empirique trois lois qui décrivent le mouvement des planètes. Ces lois furent publiées dans Astronomia Nova en 1609 et confirmèrent la théorie héliocentrique de Nicolas Copernic.
|
|
|
|
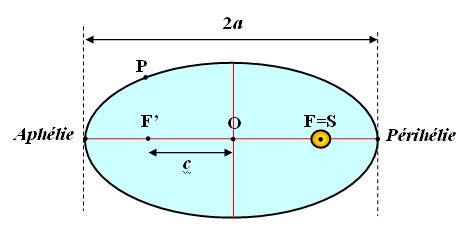
Première loi : la loi des orbites Dans le référentiel héliocentrique, la trajectoire du centre d'une planète est une ellipse dont le centre du Soleil est l'un des foyers.
|
Tout point P de l'ellipse vérifie l'égalité : PF +PF' = 2a |
|
|
Deuxième loi : la loi des aires Le rayon vecteur SP qui relie le centre S du Soleil et le centre P de la planète balaie des aires égales pendant des durées égales. Dans le référentiel héliocentrique, la vitesse de la planète devient donc plus grande lorsqu'elle se rapproche du Soleil. Elle est maximale au périhélie (position la plus proche du Soleil) et minimale à l'aphélie (position la plus éloignée du Soleil).
Troisième loi : la loi des périodes Le carré de la période de révolution T d'une planète autour du Soleil est proportionnel au cube du demi-grand axe a de l'ellipse : Cette loi, appelée également "loi harmonique de Képler", est de nature différente des deux précédentes car elle unifie le mouvement de toutes les planètes en une loi universelle. En effet, quelles que soient les planètes choisies, le rapport |
||
est le même. Il ne dépend pas de la planète mais uniquement des caractéristiques du Soleil.