Datation K/Ar

• Objectif de l'activité : réaliser la datation K/Ar d'échantillons prélevés dans la formation de Lukeino à l'aide d'un tableur.

• Compétences travaillées (il s'agit de 3 capacités et d'une attitude) :

- S'APPROPRIER : Se mobiliser en cohérence avec les consignes données (agir selon les consignes, saisir les informations utiles).
- REALISER  : Utiliser l'outil informatique.
- ANALYSER : Extraire des informations et les exploiter.
- SAVOIR-ETRE : Etre autonome.

• Activité :

La méthode potassium-argon (K-Ar) est une méthode de datation isotopique mise au point en 1948 par Aldrich et Nier. Elle peut couvrir la quasi totalité des âges géologiques avec une bonne précision. Elle repose sur la mesure de la quantité d'argon (⁴⁰Ar) et de potassium 40 (⁴⁰K) présente dans un échantillon de roche provenant de la solidification d'un magma entièrement dégazé. Elle permet de dater les minéraux des roches métamorphiques et des roches volcaniques.

Le potassium K (de numéro atomique Z= 19) possède 3 isotopes naturels : ³⁹K (93,2581 %), ⁴⁰K (0,001167%) et ⁴¹K (6,7302 %). Les roches volcaniques contiennent l'isotope 40 du potassium qui est radioactif et se désintègre selon deux voies :

- 88 % des noyaux de potassium 40 se transforment en ⁴⁰Ca (calcium 40) :

C'est une désintégration radioactive de type ß^- qui libère des électrons. La constante de désintégration est = 4,962.10^-10 a^-1 ce qui donne une période radioactive T = 1,40 Ga.

- 12 % des noyaux de potassium 40 se transforment en ⁴⁰Ar (argon) par capture d'une partie des électrons ainsi produits (on parle de radiocativité par capture électronique) :

La constante de désintégration est = 0,581.10^-10 a^-1 ce qui donne une période radioactive T = 11,9 Ga (milliards d'années).

L'argon est un gaz qui est en général retenu par les roches. Lors d'une éruption, la roche perd l’argon 40 : on parle de "dégazage." A la date de l'éruption, la lave ne contient donc plus d'argon. Au cours du temps l'argon 40, produit par la désintégration radioactive du potassium 40, va donc s'accumuler à nouveau dans la roche tandis que le potassium 40 disparaît peu à peu. Pour appliquer cette méthode, on fait donc l'hypothèse que la roche analysée ne contenait pas d'argon au moment de sa formation.

Connaissant les quantité de matière de potassium ⁴⁰K et d'argon ⁴⁰Ar d'un échantillon, on peut calculer l'âge t de de la roche ou du minéral analysé grâce à la formule chronométrique suivante (pour voir la démonstration).

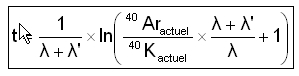
Questions :

1. Ouvrir le tableur open office et ouvrir le fichier suivant : orrorin.ods
    
2. La colonne J permet de calculer la quantité de potassium 40 connaissant le % massique de potassium K contenu dans la roche et la part du ⁴⁰K dans le K total (abondance isotopique égale à 0,01167 %). Programmer la cellule J11, sachant que n(⁴⁰K) = m (⁴⁰K) /M(⁴⁰K) et que m (⁴⁰K) = % massique de K x abondance isotopique. On précise que la masse molaire M(⁴⁰K) = 40 g/mol. Recopier la formule vers le bas à l'aide de la poignée de recopie.
   
    
3. La colonne K permet de calculer la quantité d'argon 40 connaissant le volume d'argon en cm³ contenu dans la roche. Programmer la cellule K11, sachant que n(⁴⁰Ar) = V (⁴⁰ar) / V_m (volume molaire des gaz dans les conditions standards de températures et de pression (CSTP)). La cellule G6 contient la valeur de V_m. Pour l'utiliser dans une formule comme une adresse absolue (pas modifiée lors de la copie), il faut insérer le symbole $ avant la référence de la ligne et de la colonne (il faut ainsi taper $G$6 comme adresse dans la formule). Recopier la formule vers le bas à l'aide de la poignée de recopie.
    
4. La colonne L permet de calculer l'âge de l'échantillon en Ma (millions d'années). Programmer la cellule L11 en utilisant la formule chronométrique. Là aussi, il faudra utiliser les adresses absolues des cellules C6 et C7 qui donnent les constantes radioactives. Recopier la formule vers le bas à l'aide de la poignée de recopie. Comme on demande un âge en million en Ma, il faudra penser à diviser l'âge par 1000000.

Pour voir la correction : télecharger la feuille de calcul complétée.

 Retour