Mesure de la constante solaire
Objectif :
- Dans un premier temps, on cherche à déterminer la quantité d’énergie reçue au sol chaque seconde par unité de surface de la planète Terre.
- Ensuite, on détermine la constante solaire en corrigeant la mesure précédente.
- On rappelle que la constante solaire (pour la Terre) est la puissance rayonnée reçue hors atmosphère par un disque de 1m2 placé perpendiculairement au rayonnement solaire à une distance de 1 u.a. du Soleil. Elle s'exprime en W.m-2.
Moyen :
On utilise une propriété du rayonnement solaire : son aptitude à chauffer un corps. On base donc le dispositif expérimental sur une méthode calorimétrique permettant de déterminer l’énergie reçue par un cylindre de laiton pour en déduire la puissance rayonnée reçue au sol par m2.
Rappels :
- En calorimétrie, on désigne par
avec m : la masse du corps en kilogramme
C : la chaleur massique du corps (C= 418 J.kg-1.K-1 pour le laiton)
- La puissance thermique reçue en W. m-2 est :
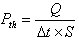(avec 
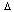t : la durée d'exposition en secondes et S : la surface exposée en m2)
La puissance thermique reçue (en W. m-2) est donc : 
Mode opératoire :
- Un cylindre de laiton peint en noir avec une peinture mate placé perpendiculairement au soleil s’échauffe. On effectue une mesure pendant 10 minutes avec le dipositif suivant. Il faut bien aligner le tube de guidage avec le Soleil. Pour éviter les pertes d'énergie par convection et rayonnement, il faut poser du cellophane transparent (type film alimentaire) sur l'extrémité avant du tube en PVC. Pour éviter les fuites par conduction, il est indispensable d'isoler la face arrière du disque de laiton (par de la mousse de polyuréthane ou du polystyrène expansé)
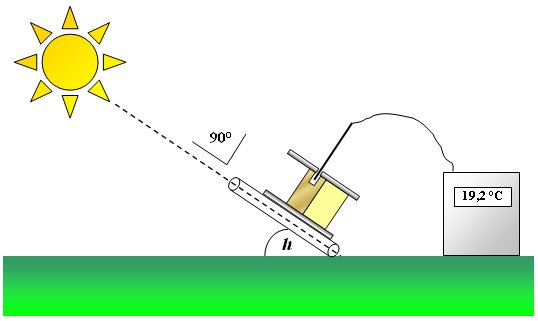
m = 157,5 g
C = chaleur massique du laiton = 418 J. Kg-1. K-1
S = 
R2 = 3,14 x (2,5.10-2)2 = 1,963.10-3 m2
t = 10 minutes = 600 secondes
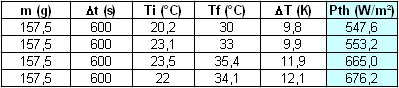
Pth est la puissance rayonnée par le Soleil reçue au sol.
Calcul de la constante solaire :
- Avant d'arriver au sol, le rayonnement solaire a été en partie absorbé par l'atmosphère. Cette absorption dépend de l'épaisseur de l'atmosphère traversée et de pureté du ciel (présence d'humidité, de poussières ...). L'épaisseur de l'atmosphère traversée dépend de l'inclinaison des rayons solaires qui est donnée par la distance zénithale z.
z = 90° - h avec h : hauteur du Soleil sur l'horizon en degrés (-90°<h<+90°)
- Le tableau suivant permet de calculer la puissance reçue par unité de surface hors atmosphère connaissant la puissance reçue par unité de surface terrestre. Il est tiré de "18 fiches d'astrophysique (classe de première S) édité par CLEA-Belin.
Distance zénithale 70° 60° 50° 40° 30° 25° Ciel pur (bleu foncé limpide) 2,50 2,00 1,70 1,50 1,35 1,30 Ciel moyen 4,2 3,5 2,6 2,1 1,8 1,5 Ciel laiteux 5,3 4,3 3,2 2,5 2,2 2,0
- Dans les conditions de l'expérience :
h = 20° (donc z = 70°) + ciel pur => correctif = x 2.5
h = 30° (donc z = 60°) + ciel pur => correctif = x 2
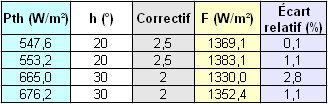
On retrouve des valeurs proches de la valeur généralement retenue : constante solaire F ≈ 1368 W.m-2.
Cette mesure peut-être réalisée par des satellites situés dans la partie supérieure de l’atmosphère. On a longtemps cru que cette valeur était pratiquement constante (d'où le nom de constante solaire). En fait, elle varie légèrement. Le projet PICARD lancé par le CNES a pour objectif d'étudier les variations de la constante solaire (appelée maintenant irradiance totale du Soleil) afin de mieux comprendre les relations entre la variabilité du Soleil et le climat terrestre.
Pour aller plus loin ...
- Puissance rayonnée par le Soleil
On utilise la constante solaire (arrondie à 1400 W.m-2) pour calculer la puissance totale rayonnée par le Soleil.
L0 ≈ 1,4 103 x 4 a2 avec a = 150. 109 mètres = distance moyenne Terre-Soleil
L0 ≈ 4. 1026 W
- Température de surface du Soleil
La puissance émise par 1 m2 de surface solaire (appelée émittance M) est :
M = L0 / (4 x RS2) = 6,5. 107 W.m-2
En considérant le Soleil comme un corps noir, on a : M =
x TS4 (loi de Stefan-Boltzmann avec = 5,67.10-8 W.m-2.K-4)
Donc TS4 = (M /)1/4 = 5800 K
- Puissance rayonnée reçue par la Terre
Si la Terre était un disque plat exposé perpendiculairement à la direction du Soleil, chaque mètre carré recevrait à chaque seconde environ 1400 W.
Mais la Terre est en fait une sphère. Chaque mètre carré de surface terrestre reçoit donc 1400 / 4 = 365 W. En effet, l’aire d’un disque est égale à R2 alors que l'aire d’une sphère est donnée par la formule : 4 R2.
Le rayon moyen de la Terre est de 6371 Km = 6,371.106 m. L’aire de la sphère terrestre correspond à 5,1.1014 m2.
La puissance rayonnée reçue par la Terre est donc : Preçue = 5,1 .1014 x 365
Preçue = 1, 86 x 1017 W
