Temperature
Calcul de la température moyenne de la Terre d'après la conférence de M. Jacques Laskar CNRS IMCCE Observatoire de Paris :
Un peu de Théorie
Pour être chauffée, une planète doit être proche d'une étoile. Considérons une planète de notre système solaire. Soit P, la quantité d'énergie solaire reçue par cette planète chaque seconde. P est une puissance rayonnée qui s'exprime en W.m-2.
On appelle constante solaire F, la quantité d'énergie reçue chaque seconde par un disque de 1 m² placé, hors atmosphère, perpendiculairement à la direction des rayons solaires à la distance de 1 U.A (unité astronomique) du Soleil.
F = 1368 W.m-2
Pour déterminer expérimentalement la constante solaire, cliquer ici.
P varie avec la distance entre le Soleil et la planète notée a. En fait, elle est inversement proportionnelle au carré cette distance. P est donc proportionnelle à F/a2.
Pour toute la surface de la planète (ici il faut considérer un disque de surface PIxR2 car F est définie pour un disque de 1 m2), on en déduit que :
(avec R : rayon de la planète en m et a : distance en U.A).
Une partie de la puissance rayonnée reçue est réfléchie par la surface selon la nature de la surface ; ainsi une surface noire ne réfléchit rien alors qu'une surface blanche réfléchit tout (notion d'albédo). On corrige donc ainsi la formule précédente en incluant ce nouveau facteur.
La puissance rayonnée incidente reçue au niveau de la surface de la planète est donc :
ou A est l'albédo de la planète (si le corps est noir A = 0)
La planète reçoit cette énergie et se réchauffe. Ainsi, elle va réémettre de l'énergie dans toutes les directions de l'espace comme un corps noir. Selon la loi de Stefan-Boltzmann, chaque mètre carré de surface réémet chaque seconde la puissance Pémis telle que :
Pémis = 
x TP4
avec TP la température absolue de surface de la planète (en K)
et la constante de Stefan-Boltzmann (=5,67.10-8 W.m-2.K-4 ).
La puissance rayonnée Pr réémise par la surface sphérique de la planète est donc :
avec : constante de Stefan-Boltzmann (=5,67.10-8 W.m-2.K-4 )
et R : rayon de la planète (en m).
La température d'équilibre radiatif de la planète s'obtient en écrivant la loi de conservation de l'énergie 
. On en déduit que :
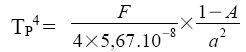
d'où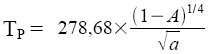 
avec a : distance Soleil-planète en U.A
