D- IRM fonctionnelle : quelques idées sur le traitement statistique des données

Le principe général d'une étude IRMf

Il consiste à analyser le signal BOLD (Blood Oxygen Level Dependent) qui traduit l'augmentation d'afflux en oxygène dans les régions cérébrales activées. Les étapes d’une analyse de données :

1. Prétraitement :

Cette étape permet de corriger au mieux les erreurs qui pourraient être introduites par la technique IRM de recueil des données.

• Correction du décalage d’acquisition entre coupes
• Correction du mouvement
• Normalisation
• Lissage spatial

2. Spécification d’un modèle

Choix des régresseurs correspondant aux différentes conditions expérimentales. Ce choix d’un modèle va permettre d’analyser le signal BOLD prétraité.

3. Estimation des paramètres du modèle

(les β dans SPM : Statistical Parametric Mapping).
Les étapes 2 et 3 correspondent à l'utilisation du Modèle Linéaire Général : GLM. Ces étapes ne sont pas abordées dans ce document.

4. Traitement statistique et visualisation

C'est la partie qui nous intéresse ici.

AVERTISSEMENT :

Ce travail ne prétend pas expliquer la réalité des traitements statistiques (fort complexes) qui sont effectués dans une étude IRMf mais seulement donner quelques idées sur l’esprit dans lequel se situent ces traitements. Nous nous placerons dans le cadre restrictif suivant :

• Expérimentation s’appuyant sur 2 conditions et 2 seulement :

Condition ON : présence du stimulus
Condition OFF : absence du stimulus

• Modélisation de chaque condition par un seul régresseur (le signal s’écrira alors Y=β₀* R₀+β_off * R_off+β_on* R_on+ ε  dans la terminologie SPM)
• Utilisation d’un test de STUDENT

Partie 1 : un peu de statistique

1. Loi de STUDENT :

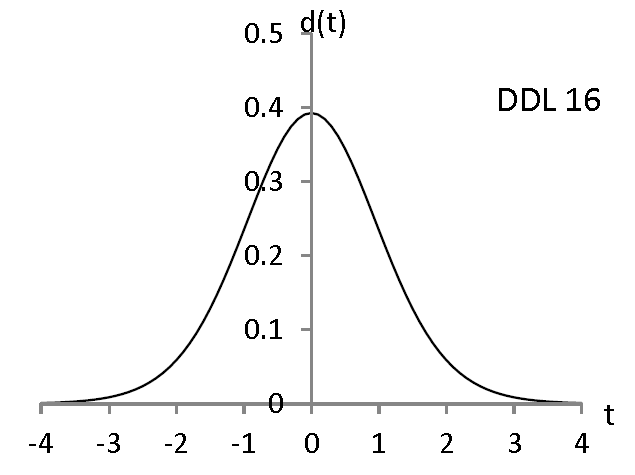
a) Une loi de Student est définie par son degré de liberté (ddl). Elle est caractérisée par une fonction appelée « densité de probabilité » : d , dont la représentation graphique a la forme d’un chapeau style bicorne, symétrique par rapport à l’axe des ordonnées.

b) On dit qu’une variable aléatoire X suit la loi de Student à n degrés de liberté lorsque pour tout nombre x :

P(X≤x) = A(x) où A(x) est l’aire de la partie du plan grisée sur le graphique ci-dessus.

( pour les matheux :  )

2. Résultat important

P1 et P2 étant deux populations sur lesquelles on mesure le même caractère quantitatif, lorsque les conditions suivantes sont réunies :

• Les populations P1 et P2 sont gaussiennes pour ce caractère (c’est-à-dire que les valeurs prises par x se répartissent en suivant une loi normale).
• La moyenne µ du caractère x est la même pour les populations P1et P2 (µ1 = µ2)
• L’écart-type σ du caractère x est le même pour les populations P1 et P2 (σ1 = σ2)

Alors la variable aléatoire T qui, à tout échantillon aléatoire E₁ de taille n₁ de la population P₁ et à tout échantillon aléatoire E₂ de taille n₂ de la population P₂, associe  , où  et  sont les moyennes du caractère x pour E₁ et E₂ , suit la loi de Student à (n₁ + n₂ - 2) degrés de liberté.

QU’EST-CE QUE CA SIGNIFIE ?

En prenant différents échantillons E₁ et E₂, ce nombre : t , va varier du SEUL FAIT DU HASARD et il ne va pas varier n’importe comment ! Les valeurs prises par T vont se répartir en suivant cette loi de Student.

3. La position du chercheur utilisant L’IRMf :

Question : Quels sont les voxels activés en présence du stimulus ?

Imaginons que l’étude IRMf débouche pour chaque voxel sur :

• Une série de mesures x_off (correspondant à la condition OFF)
• Une série de mesures x_on (correspondant à la condition ON)

Le même traitement est effectué pour tous les voxels, concentrons-nous maintenant sur l’un d’eux.
 

POUR UN VOXEL, nous avons 2 séries de mesures :

x_off1 ; x_off2 ;……… ; x_off,_{n off} et x_on1 ; x_on2 ;……… ; x_{on,n on}

Exemple numérique :
 

Nous avons ci-dessus n_off=10 mesures en condition OFF et n_on=8 mesures en condition ON.
 

Ce sont les valeurs prises par x pour des échantillons E_off et E_on des populations P_off et P_on de toutes les mesures qu’on aurait pu faire dans les conditions OFF et ON.
Nous pouvons facilement calculer les moyennes : et  ainsi que les écarts-type s_off et s_on pour ces deux échantillons.

Exemple numérique :

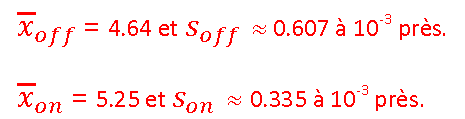
Par contre, nous ne connaissons pas les moyennes μ_off et μ_on des mesures x pour les populations P_off et P_on !
Et pourtant, c’est bien la comparaison entre μ_off et μ_on (sur les populations globales) qui permettrait de répondre à la question : le voxel est-il activé en présence du stimulus ?

QUE FAIRE ? UN TEST DE VALIDITE D’HYPOTHESE UNILATERAL: DANS NOTRE CAS, CE SERA UN TEST DE STUDENT.

Comment ça marche ?

1ère étape :

Il y a d’abord 2 présupposés :
Les populations P_off et P_on sont gaussiennes pour les mesures x.
Les écarts-types 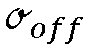et 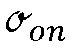des populations P_off et P_on sont égaux (ce point peut être testé au préalable).

On estime alors cet écart-type commun par :

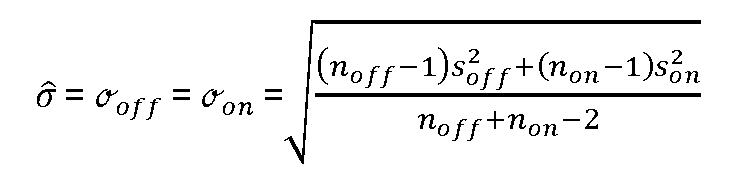
Exemple numérique :

2ème étape : formulation des hypothèses

• Hypothèse nulle : µ_on = µ_off , soit µ_on - µ_off = 0 (le voxel n’est pas activé)
• Hypothèse alternative : µ_on > µ_off , µ_on - µ_off  > 0 (le voxel est activé)

(Dans SPM, en écrivant 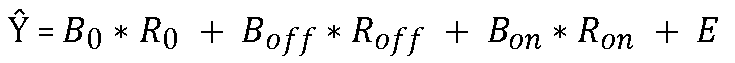, l’hypothèse nulle est : B_on = B_off et l’hypothèse alternative est : B_on > B_off )

3ème étape : règle de décision et décision

Sous l’hypothèse nulle (µ_on = µ_off, pas d’activation) , la variable aléatoire qui , à tout échantillon de n_off mesures x_off et à tout échantillon de n_on mesures x_on , associe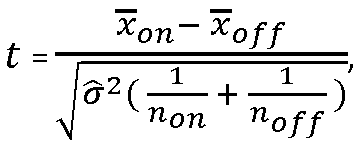, suit la loi de Student à (n_off + n_on - 2) degrés de liberté (nous l’avons affirmé au 1.2).
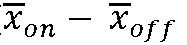( correspond dans SPM à β_on – β_off ; à la différence notable que les β représentent la contribution des différentes conditions expérimentales aux variations du signal )

Exemple numérique :

Sous l’hypothèse nulle (µ_on = µ_off, pas d’activation) , la variable aléatoire qui , à tout échantillon de 10 mesures x_off et à tout échantillon de 8 mesures x_on, associe 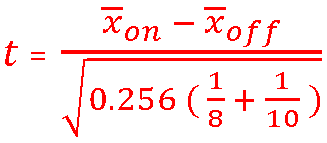,suit la loi de Student à (10+8 -2) = 16 degrés de liberté.

Déterminons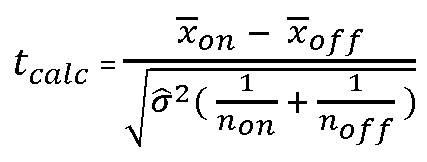 avec nos mesures.
 

Exemple numérique :

Il est très improbable de trouver exactement 0 même si le voxel n’est pas activé.

Toute la difficulté est la suivante : l’écart entre t_calc et 0, vais-je décider de l’attribuer au seul hasard ou pas ? En d’autres termes, vais-je décider de déclarer le voxel activé ou pas ?

ICI EST LE POINT CRUCIAL POUR COMPRENDRE N’IMPORTE QUEL TRAVAIL D’INFERENCE STATISTIQUE.

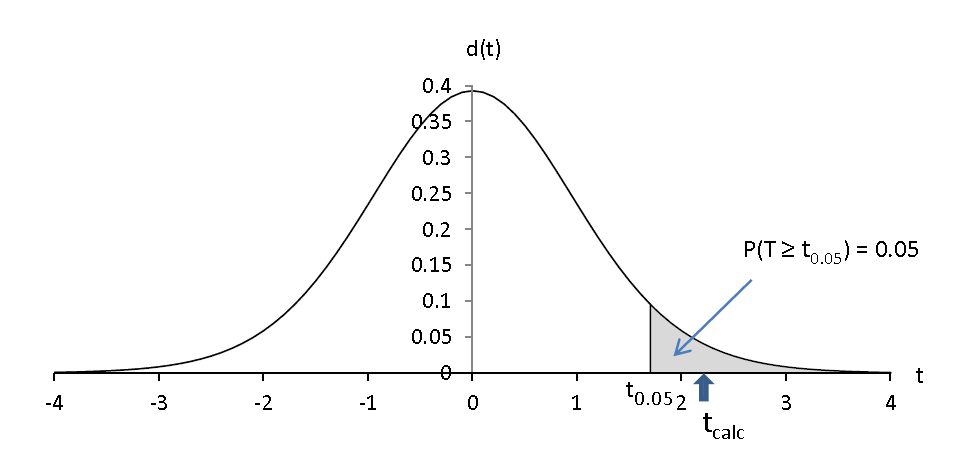
Sous l’hypothèse nulle, la loi de Student à (n_off + n_on - 2) degrés de liberté nous permet de calculer, A PRIORI, la probabilité que T prenne une valeur dans n’importe quel intervalle de notre choix, elle nous permet en particulier de déterminer la valeur t telle que P(T ≥ t) soit égal à une valeur α donnée (avec 0 < α < 1).

Par exemple :
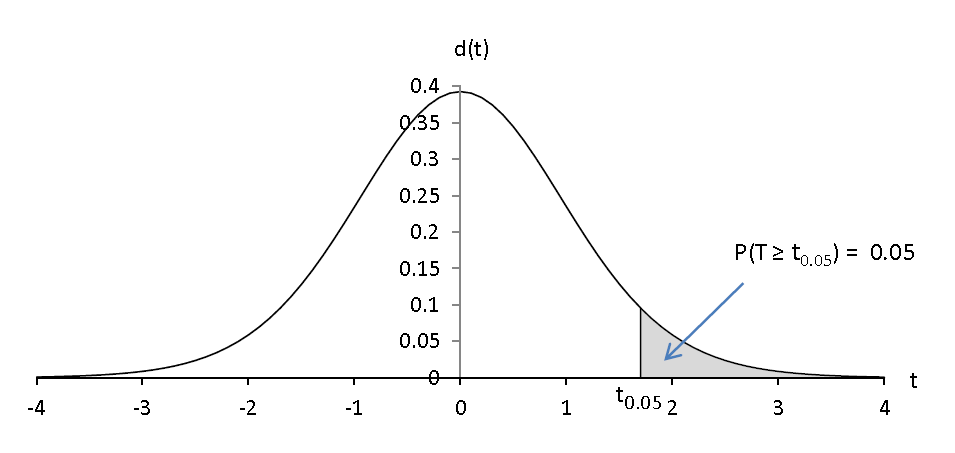
Pour α = 0.05

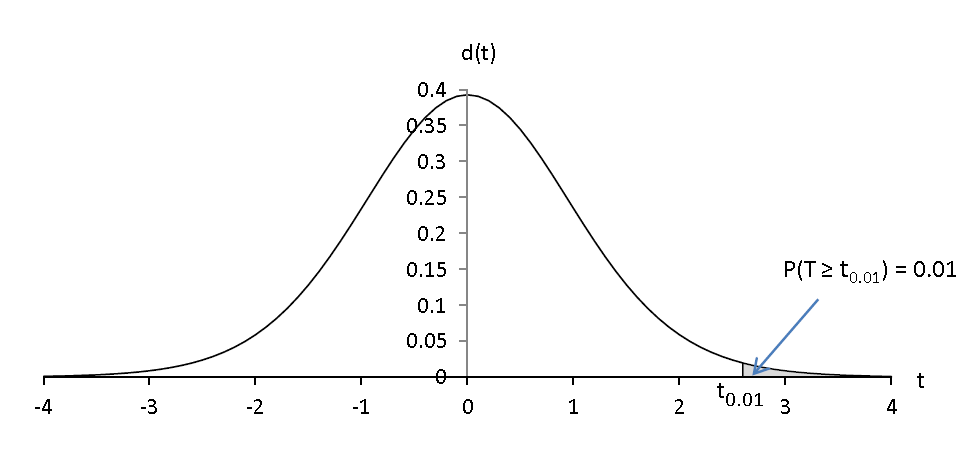
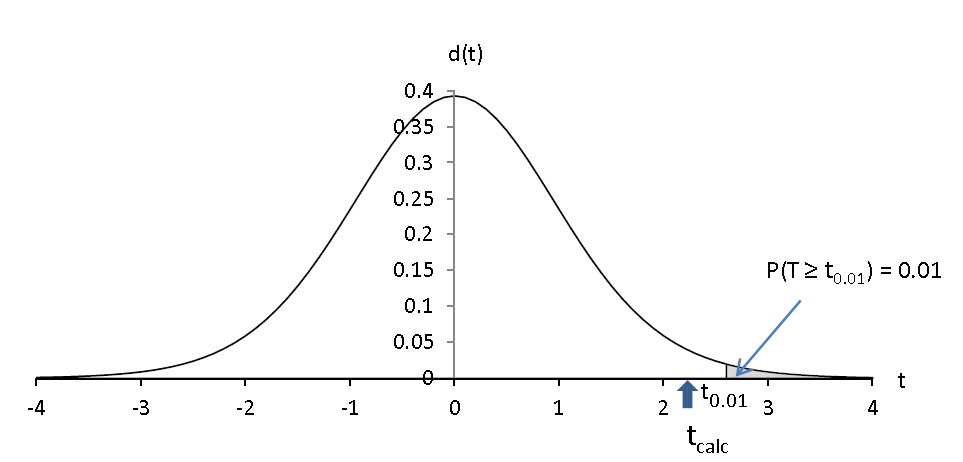
Pour α = 0.01

QU’EST CE QUE CA SIGNIFIE ?

Avant mon expérimentation , en admettant que le voxel n’est pas activé , je peux affirmer que j’ai 5 chances sur 100 pour que la valeur de t_calc soit supérieure à t_0.05 ; je peux affirmer que j’ai 1 chance sur 100 pour que la valeur de t_calc soit supérieure à t_0.01.

De façon générale, nous pouvons, sous l’hypothèse nulle, calculer t_α tel que P(T ≥  t_α) = α ; α est appelé : seuil de risque.

ET MAINTENANT IL S’AGIT DE DECIDER !

Revenons au t_calc que nous avons déterminé. Quel est le raisonnement ?

• Au seuil 0.05 , je n’avais sous l’hypothèse nulle que 5 chances sur 100 pour que la valeur de t_calc soit supérieure à t_0.05. Or elle l’est. Je refuse donc l’hypothèse nulle et j’affirme, au seuil 0.05 , que le voxel est significativement activé .

• Au seuil 0.01 , j’avais  sous l’hypothèse nulle 1 chance sur 100 pour que la valeur de t_calc soit supérieure à t_0.01 et elle ne l’est pas. J’accepte donc l’hypothèse nulle et j’affirme, au seuil 0.01 , que le voxel  n’est pas significativement activé .

 Pour être certain d’avoir bien compris la démarche, faisons des choix extrêmes :

• Seuil de risque : 0

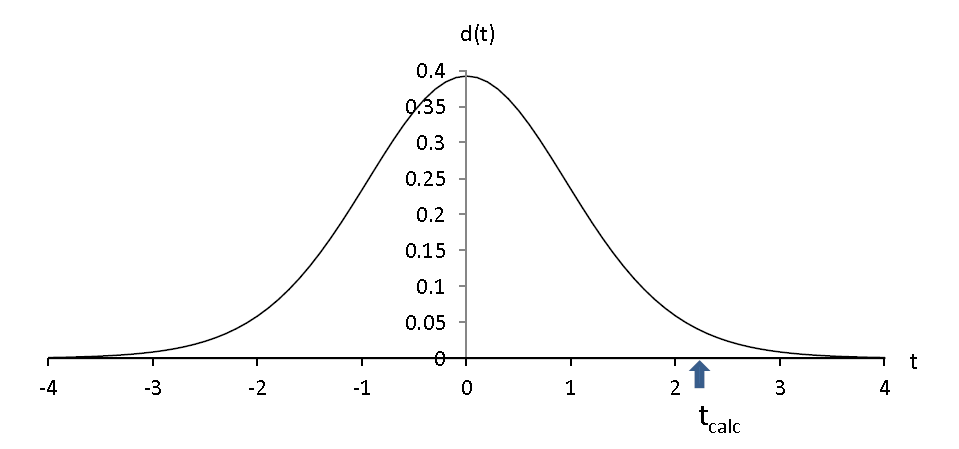
 On a t₀= +∞
L’hypothèse nulle est systématiquement validée !

Je peux affirmer, au seuil de risque 0 , qu’aucun voxel n’est activé ! Il n’est pas utile de faire une expérimentation.

AUCUN INTERET !

• Seuil de risque : 1

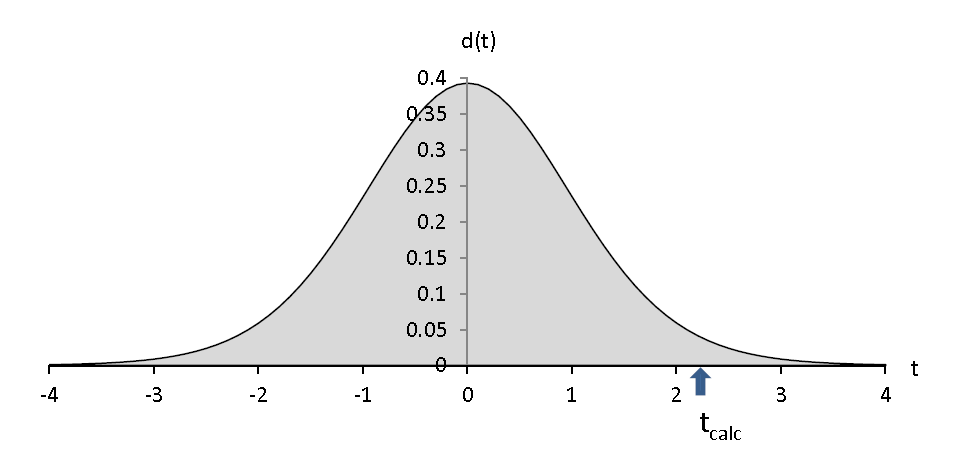
On a t₁ = - ∞
L’hypothèse nulle est systématiquement rejetée !
Je peux affirmer, au seuil de risque 1 que tous les voxels sont activés !

AUCUN INTERET NON PLUS !
 

ATTENTION :
Le sens commun voudrait que plus un seuil de risque est choisi proche de 0 , plus les conclusions d’une étude soient fiables . Ce n’est malheureusement pas si simple !
Dans ce qui suit nous éviterons l’expression « seuil de risque », qui peut induire des idées fausses. Nous utiliserons à sa place le mot « seuil ».
 

RESUME :

Nous choisissons un seuil α.
Nous déterminons t_α tel que P(T ≥ t_α ) = α

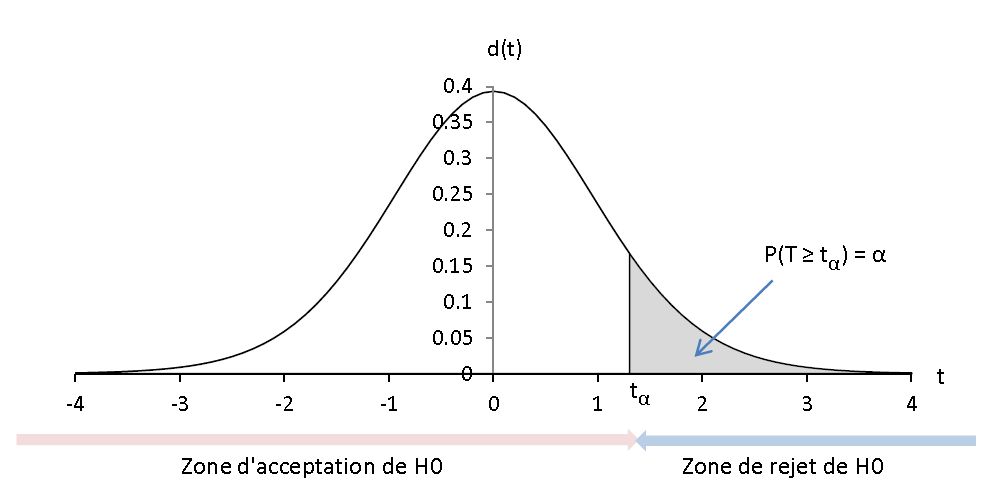
• Si t_calc ≤ t_α nous acceptons H0 et affirmons au seuil α que le voxel n’est pas significativement activé.
• Si  t_calc > t_α nous rejetons H0 et affirmons au seuil α que le voxel est significativement activé.

Exemple numérique :
t_calc ≈ 2.542 à 10^-3 près.
Pour le degré de liberté : 16
t_0.05 ≈ 1.746 à 10^-3 près donc t_calc > t_0.05
nous rejetons H0 et affirmons au seuil 0.05 que le voxel est significativement activé.
t_0.01 ≈ 2.583 à 10^-3 près donc t_calc  ≤ t_0.01
nous acceptons H0 et affirmons au seuil 0.01 que le voxel n’est pas significativement activé.

REMARQUE :
Il s’agit bien d’une décision ; la réalité ne peut pas être connue en toute certitude, à partir d’inférences statistiques.
Le choix du seuil est capital dans le processus de décision et il n’est pas imposé d’un strict point de vue mathématique.

Partie 2 : Les images en IRMf

Si les données IRMf étaient traitées comme nous venons de l’expliquer, nous aurions des images en noir et blanc, voire bicolores, mais pas de niveaux de gris, pas d’échelles de couleurs.

En effet, chaque voxel, suite au test de Student, serait déclaré activé ou pas. C’est en partie le cas mais ça n’est pas uniquement ça !

• Encore un petit peu de statistiques
• Le choix de SPM
• Comment sont construites les images

1. Encore un petit peu de statistiques :

Courage, on y est presque !
Il existe une autre possibilité d’utiliser la loi de Student :
Partons de notre expérimentation, pour un voxel nous avons déterminé t_calc .

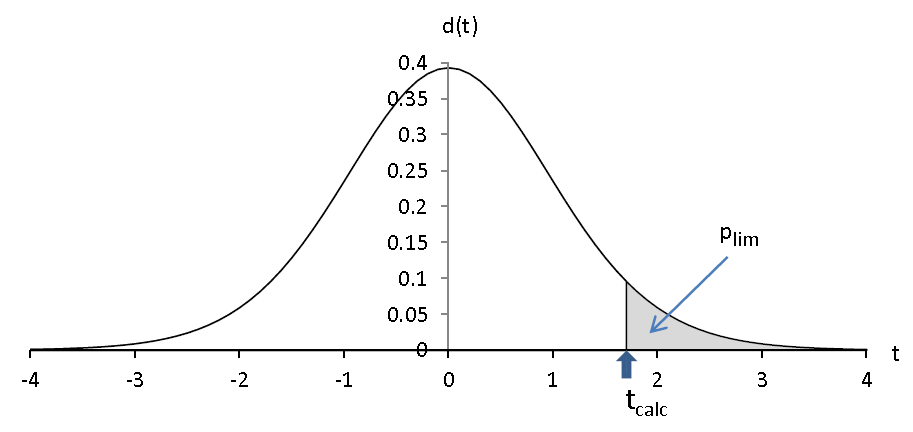
Nous pouvons, connaissant le degré de liberté, calculer p_lim⁡ = P (T ≥ t_calc) .

Quel sens donner à ce p_lim ? (il correspond au p_uncorrected de SPM)

• pour un seuil p_lim + ε (ε > 0) :

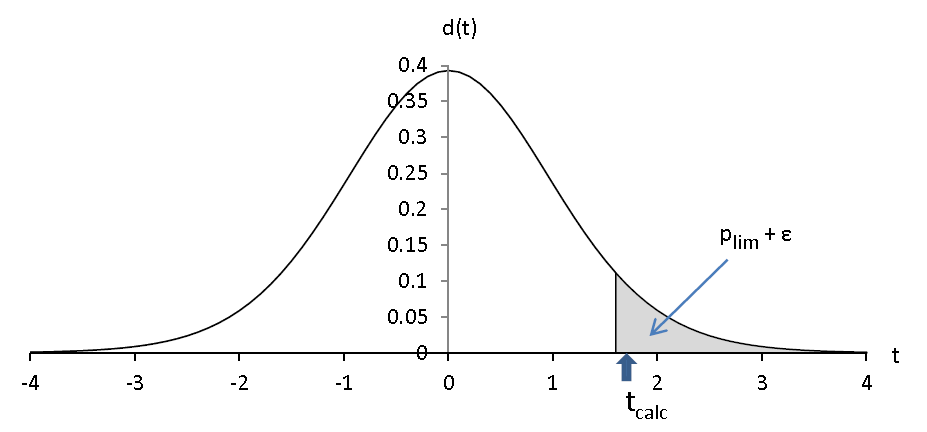
Nous affirmerions, à ce seuil, que le voxel est significativement activé.

• pour un seuil p_lim - ε (ε > 0) :

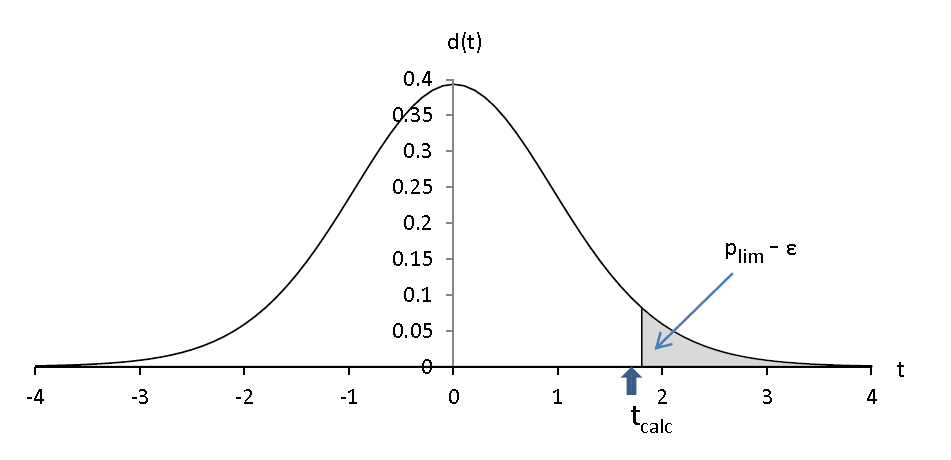
Nous affirmerions, à ce seuil, que le voxel n’est pas significativement activé.
En résumé, c’est le seuil qui correspond à l’inversion de la décision.

Exemple numérique :
Avec DDL = 16 et t_calc = 2.542 on obtient p_lim ≈ 0.01088 à 10^-5 près.
 

2. Le choix de SPM :

Nous pourrions donc pour représenter l’activation neuronale au sein de chaque voxel, choisir de créer une image à partir de ces valeurs p_lim. Ce n’est pas le choix de SPM.
En fait, pour un « contraste » donné (par exemple comparaison entre conditions ON et OFF) , le degré de liberté est le même pour tous les voxels du « masque » (ensemble de tous les voxels pris en compte dans le traitement). Les t_calc et les p_lim sont en parfaite correspondance (p_lim=f(t_calc) où f est une fonction continue et strictement décroissante). Nous pouvons donc nous contenter de représenter dans les images, les valeurs de t_calc. C’est ce que fait SPM.

PAR CONTRE : Du fait des différences de degrés de liberté entre divers « contrastes », il serait illégitime de comparer des images d’activation même en les seuillant de façon identique.
C’est envisageable, d’un point de vue statistique, en se référant aux p_lim qui, eux, ont un sens indépendamment du degré de liberté.

3. Comment sont construites les images ?

Pour un « contraste » donné, nous avons un fichier contenant les valeurs de t_calc pour tous les voxels du « masque ». Nous connaissons de plus le degré de liberté correspondant à ce « contraste ».

Admettons par exemple : ddl = 20

Si nous choisissons un seuil α = 0.01 alors t_0.01 ≈ 2.528

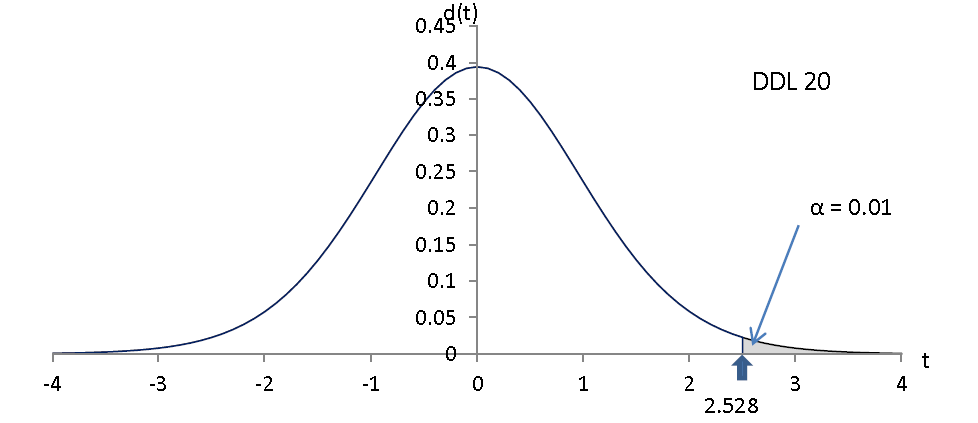
• Les voxels pour lesquels t_calc ≤ 2.528 ne sont pas significativement activés au seuil 0.01. ILS SONT TRANSPARENTS SUR L’IMAGE IRMf (ils n’apparaissent pas).
• Les voxels pour lesquels t_calc > 2.528 sont significativement activés au seuil 0.01. ILS SONT REPRESENTES SUR L’IMAGE. La couleur correspondant à chacun d’eux est définie grâce à l’échelle de couleurs :

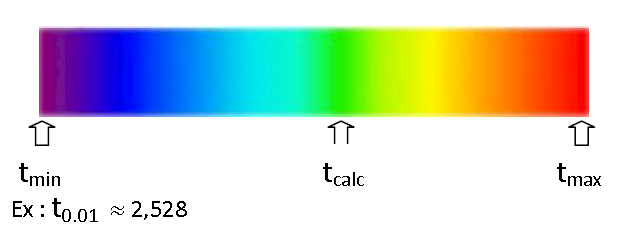
La valeur choisie pour t_max a une incidence sur la répartition des couleurs mais n’appelle pas de commentaire particulier à l’exception de celui-ci : les voxels pour lesquels t_calc ≥ t_max sont représentés sur l’image avec la couleur correspondant à t_max (ici : rouge)
 

QUELLES SONT LES CONSEQUENCES DU CHOIX DE t_min ?

Dans SPM, au moment de visualiser les résultats, nous choisissons t_min ; de ce choix dépend l’image produite mais cette valeur n’est pas facile à interpréter ! Il est cependant toujours possible de retrouver le seuil α = α_tmin correspondant à t_min (en utilisant EXCEL par exemple : voir annexe) car nous connaissons le ddl de la loi de Student correspondant au « contraste ».

Ce seuil α = α_tmin, lui, est assez facile à interpréter :

Reprenons l’exemple précédent.

Choisissons α = 0.01 :

• Pour un voxel donné, en supposant qu’il ne soit pas activé, la probabilité que t_calc > 2.528 est 0.01. J’aurais donc, dans ce cas, 1 chance sur 100 de le déclarer significativement activé et de le faire apparaitre en tant que tel sur l’image.
• Pour l’ensemble de tous les voxels du « masque », en supposant qu’aucun d’eux ne soit activé, je peux m’attendre à en déclarer 1 % significativement activés et à les faire apparaitre en tant que tels sur l’image.

Choisissons maintenant α = 0.001 : avec ddl=20 t_0.001 ≈ 3.552

• Pour un voxel donné, en supposant qu’il ne soit pas activé, la probabilité que t_calc > 3.552 est 0.001. J’aurais donc, dans ce cas, 1 chance sur 1000 de le déclarer significativement activé et de le faire apparaitre en tant que tel sur l’image.

CE SEUIL EST PLUS CONTRAIGNANT POUR DECLARER QU’UN VOXEL EST ACTIVE. JE MINIMISE PAR CE CHOIX LE RISQUE DE DECLARER A TORT QU’UN VOXEL EST ACTIVE ET DE LE REPRESENTER EN TANT QUE TEL SUR L’IMAGE, PAR CONTRE J’AUGMENTE LE RISQUE DE DECLARER A TORT QU’IL NE L’EST PAS ET DE NE PAS LE REPRESENTER SUR L’IMAGE ALORS QU’IL DEVRAIT L’ETRE. ETERNEL DILEMME !

• Pour l’ensemble de tous les voxels du « masque », en supposant qu’aucun d’eux ne soit activé, je peux m’attendre à n’en déclarer que 0. 1 % significativement activés et à les faire apparaitre en tant que tels sur l’image.

Remarques :
Les seuils α = α_tmin couramment utilisés lors de la production d’images IRMf semblent être de l’ordre de 0.001, ce qui minimise le risque de « faux positifs », au détriment des « faux négatifs » bien sûr.

Le degré de liberté du GLM (Modèle Linéaire Général) correspondant aux études IRMf utilisant un test de Student, se situe dans la plupart des cas entre 100 et 1000 pour les études sur un individu et entre 15 et 30 ou plus pour les études de groupes. Ce sont ces dernières qui sont le plus souvent présentées dans les études scientifiques.

Télécharger l'intégralité du dossier (format .pdf)